Решение логических задач первый шаг к развитию ребенка

Решение задач на логику — отличная гимнастика для ума детей и взрослых на каждый день.
На ЛогикЛайк более 3500 заданий с ответами и пояснениями, полноценный учебный комплекс для развития логики и способностей к математике.
Решаем логические задачи
Чтобы научиться решать типовые логические задачи, простые и нестандартные математические задачи, важно знать основные приемы и методы их решения. Ведь решить одну и ту же задачу и прийти к правильному ответу во многих случаях можно разными способами.
Знание и понимание различных методов решения поможет определить, какой способ подойдет лучше в каждом конкретном случае, чтобы выбрать наиболее быстрый и простой путь получения ответа.
К «классическим» логическим задачам относятся текстовые задачи, цель решения которых состоит в распознавании объектов или расположении их в определенном порядке в соответствии с заданными условиями.
Более сложными и увлекательными типами заданий являются задачи, в которых отдельные утверждения являются истинными, а другие ложными. Задачи на перемещение, перекладывание, взвешивание, переливание — самые яркие примеры широкого ряда нестандартных задач на логику.
Основные методы решения логических задач
- метод рассуждений;
- с помощью таблиц истинности;
- метод блок-схем;
- средствами алгебры логики (алгебры высказываний);
- графический (в том числе, «дерево логических условий», метод кругов Эйлера);
- метод математического бильярда.
Давайте рассмотрим подробнее с примерами три популярных способа решения логических задач, которые мы рекомендуем использовать в начальной школе (детям 6-12 лет):
- метод последовательных рассуждений;
- разновидность метода рассуждений — «с конца»;
- табличный способ.
Метод последовательных рассуждений
Самый простой способ решения несложных задач заключается в последовательных рассуждениях с использованием всех известных условий. Выводы из утверждений, являющихся условиями задачи, постепенно приводят к ответу на поставленный вопрос.
Пример:
На столе лежат Голубой, Зеленый, Коричневый и Оранжевый карандаши.
Третьим лежит карандаш, в имени которого больше всего букв. Голубой карандаш лежит между Коричневым и Оранжевым.
Разложи карандаши в описанном порядке.

Решение:
Рассуждаем. Последовательно используем условия задачи для формулирования выводов о позиции, на которой должен лежать каждый следующий карандаш.
- Больше всего букв в слове «коричневый», значит, он лежит третьим.
- Известно, что голубой карандаш лежит между коричневым и оранжевым. Справа от коричневого есть только одна позиция, значит, расположить голубой между коричневым и другим карандашом возможно только слева от коричневого.
- Следующий вывод на основе предыдущего: голубой карандаш лежит на второй позиции, а оранжевый — на первой.
- Для зеленого карандаша осталась последняя позиция — он лежит четвертым.
Метод «с конца»
Такой способ решения является разновидностью метода рассуждений и отлично подходит для задач, в которых нам известен результат совершения определенных действий, а вопрос состоит в восстановлении первоначальной картины.
Пример:
Бабушка испекла для троих внуков рогалики и оставила их на столе. Коля забежал перекусить первым. Сосчитал все рогалики, взял свою долю и убежал.
Аня зашла в дом позже. Она не знала, что Коля уже взял рогалики, сосчитала их и, разделив на троих, взяла свою долю.
Третьим пришел Гена, который тоже разделил остаток выпечки на троих и взял свою долю.
На столе осталось 8 рогаликов.
Сколько рогаликов из восьми оставшихся должен съесть каждый, чтобы в результате все съели поровну?

Решение:
Начинаем рассуждение «с конца».
Гена оставил для Ани и Коли 8 рогаликов (каждому по 4). Получается, и сам он съел 4 рогалика: 8 + 4 = 12.
Аня оставила для братьев 12 рогаликов (каждому по 6). Значит, и сама она съела 6 штук: 12 + 6 = 18.
Коля оставил ребятам 18 рогаликов. Значит, сам съел 9: 18 + 9 = 27.
Бабушка положила на стол 27 рогаликов, рассчитывая, что каждому достанется по 9 штук. Поскольку Коля уже съел свою долю, Аня должна съесть 3, а Гена — 5 рогаликов.
Решение логических задач с помощью таблиц истинности
Суть метода состоит в фиксации условий задачи и полученных результатов рассуждений в специально составленных под задачу таблицах. В зависимости от того, является высказывание истинным или ложным, соответствующие ячейки таблицы заполняются знаками «+» и «-» либо «1» и «0».
Пример:
Три спортсмена (красный, синий и зеленый) играли в баскетбол.
Когда мяч оказался в корзине, красный воскликнул: «Мяч забросил синий».
Синий возразил: «Мяч забросил зеленый».
Зеленый сказал: «Я не забрасывал».
Кто забросил мяч, если только один из троих сказал неправду?
Решение:
Сначала таблицу составляют: слева записывают все утверждения, которые содержатся в условии, а сверху — возможные варианты ответа.

Затем таблицу последовательно заполняют: верные утверждения отмечают знаком «+», а ложные утверждения — знаком «-«.

Рассмотрим первый вариант ответа («мяч забросил красный«), проанализируем утверждения, записанные слева, и заполним первый столбик.
Исходя из нашего предположения («мяч забросил красный«), утверждение «мяч забросил синий» — ложь. Ставим в ячейке «-«.
Утверждение «мяч забросил зеленый» также ложь. Заполняем ячейку знаком «-«.
Утверждение зеленого «Я не забрасывал» – истина. Ставим в ячейке «+».
Рассмотрим второй вариант ответа (предположим, что мяч забросил зеленый) и заполним второй столбик.
Утверждение «мяч забросил Синий» — ложь. Ставим в ячейке «-«.
Утверждение «мяч забросил зеленый« — истина. Заполняем ячейку знаком «+».
Утверждение зеленого «Я не забрасывал» – ложь. Ставим в ячейке «-«.
И, наконец, третий вариант: предположим, что «мяч забросил синий«.
Тогда утверждение «мяч забросил синий« — истина. Ставим в ячейке «+».
Утверждение «мяч забросил зеленый» — ложь. Заполняем ячейку знаком «-«. Утверждение зеленого «Я не забрасывал» – истина. Ставим в ячейке «+».
Так как по условию лишь один из троих ребят сказал неправду, в заполненной таблице выбираем такой вариант ответа, где будет только одно ложное утверждение (в столбце один знак «-«). Подходит третий столбец.
Значит, правильный ответ – мяч забросил синий.
Метод блок-схем
Метод блок-схем считается оптимальным вариантом для решения задач на взвешивание и на переливание жидкостей. Альтернативный способ решения этого типа задач — метод перебора вариантов — не всегда является оптимальным, да и назвать его системным довольно сложно.
Порядок решения задач по методу блок-схем выглядит следующим образом:
- графически (блок-схемой) описываем последовательность выполнения операций;
- определяем порядок их выполнения;
- в таблице фиксируем текущие состояния.
Подробнее об этом и других способах решения логических задач с примерами и описанием хода решения мы рассказываем в полном Курсе ЛогикЛайк по развитию логического мышления.
Отгадывайте самые интересные загадки на логику, собранные специально для постоянных читателей нашего блога и учеников LogicLike, решайте логические задачи онлайн вместе с тысячами детей и взрослых!
Источник
Дети с развитой логикой смогут решить любую задачу
Развивать логическое мышление учащихся начальных классов необходимо постоянно. Регулярные тренировки в решении головоломок, нестандартных задач, ребусов и задач на смекалку полезны и необходимы для ума ребенка.
Для развития логического мышления младших школьников используются несложные задания, например, найти лишнее, продолжить ряд знаков, найти числа или недостающие фигуры и т.д. Даже самые простые логические задачи для детей помогают избавить мышление от шаблонов.
Что должен уметь школьник для успешного выполнения заданий на логику?
- рассуждать, используя доказательства и аргументы;
- последовательно мыслить;
- выстраивать гипотезы;
- оценивать важность условий задачи, их истинность;
- аргументированно опровергать чужие неверные выводы;
- выбирать и использовать разные способы для решения конкретного вида задач.
Способы решения задач на логику
Условно их можно поделить на стандартные и нестандартные.
Стандартные методы
К традиционным методам относятся популярный метод проб и ошибок, который может потребовать много времени и терпения, и метод шаблонов, к которому в основном прибегают при решении школьных задач.
Мы знаем, что абсолютное большинство взрослых захотят решить предложенную задачу с помощью уравнения. Неплохой способ, но зачастую обыкновенные логические рассуждения помогают найти ответ быстрее, без ручки и бумаги, просто в уме.
Рекомендуем ознакомиться с несколькими популярными методами, описанными на примерах в материале «Как решать логические задачи»:
- метод последовательных рассуждений;
- «с конца»;
- с помощью таблиц истинности;
- метод блок-схем.
Нестандартные методы
Среди популярных, нестандартных — целенаправленный поиск «ключа» («ключей») и метод «игры в создателя» (т.е. моделирования различных вариантов принципов, использованных для создания задачи). А если подсказки, шаблоны решения отсутствуют, применяется самый сложный метод – поиска метода.
Для быстрого и правильного решения различных логических головоломок и задач на смекалку ребенку необходимо:
- знать виды логических задач;
- владеть возможными методами решения задач;
- уметь классифицировать задачу и выбирать самый простой и «красивый» способ ее решения.
Алгоритм решения задач на логику и смекалку
Основные шесть этапов, которые последовательно должен пройти ученик, решая логическую задачу:
- Ознакомление с условиями задачи.
- Понимание содержания задачи, анализ условий, моделирование.
- Поиск метода решения.
- Применение метода решения, поиск правильного ответа.
- Проверка правильности решения и оформление ответа.
- Анализ проведенного решения.
- Отработка и закрепление навыков решения аналогичных задач.
1. Внимательно прочитайте условие задачи, лучше несколько раз. Четко уясните вопрос или проблему, которую нужно разрешить. Чаще всего ошибки в решении появляются от невнимательности. Особенно это касается задач с подвохом.
2. Кратко запишите условия задачи, по возможности, опишите задачу схематически (в виде рисунка, схемы, графика, дерева, чертежа и т.д.). Наглядное представление задачи не только способствует более быстрому уяснению содержания задачи, но и поможет выявить новые связи между элементами задачи или увидеть скрытые свойства объектов. Выделите существенные и несущественные условия задачи и попробуйте упростить задачу, абстрагироваться от действительности, мысленно смоделировать описанную в задаче ситуацию.
3. Попытайтесь определить тип задачи и соответственно подобрать метод решения, который обычно применяется для решения этого вида заданий. Например, для решения задач на определение истинности или ложности высказывания удобно использовать таблицу. Для решения задач с большим количеством взаимосвязанных условий лучше использовать метод графов и т.д.
4. Используя выбранный метод, решите задачу.
5. Проверьте ваш вариант ответа. В случае письменного решения задачи надлежащим образом запишите правильный ответ.
6. Анализ проведенного решения представляет собой обсуждение всего хода мыслительных действий в процесс решения логической задачи. Это завершающий и необходимый этап решения любой задачи, не только логической. Он включает:
- поиск альтернативного, более рационального, красивого способа решения;
- анализ всего процесса, моментов, которые вызвали затруднения;
- выделение важных признаков данного типа задач;
- составление алгоритма их решения;
- систематизация полученных знаний.
Школьнику полезно записывать свои решения, алгоритмы и рассуждения в отдельную тетрадь, например, специально для занятий на ЛогикЛайк. Таким образом он будет «пропускать через моторику» свои рассуждения и всегда сможет вернуться к своим наработкам.
7. Чтобы закрепить свое умение решать головоломки определенного типа, необходимо не откладывая решить еще ряд подобных, однотипных задач с постепенным усложнением набора условий.
В учебной программе образовательной платформы LogicLike логические задачи распределены по 15 тематическим разделам. Каждая категория содержит задания разного уровня сложности.
Таким образом осуществляется последовательное и системное развитие логического мышления младших школьников. Подробнее о курсе развития логического мышления.
Чтобы занятия ребенка логикой были эффективнее, рекомендуем родителям дошкольников и первоклассников заниматься вместе с детьми.
Правильный подход к учебному процессу поможет научить ребенка решать логические задачи и воспитать полезные ему качества.
В ходе обучения на ЛогикЛайк дети становятся более самостоятельными и уверенными в себе, воспитывают в себе ответственность за принимаемые решения, усидчивость и настойчивость.
Источник
Логика – это основа рационального мышления и фундамент для развития интеллекта ребенка. Решение различных логических задач дает возможность детям научиться анализировать ситуацию, находить взаимосвязи, отличать главное и второстепенное, формировать стратегию, применять в нужном месте свои знания и навыки.
Эти умения пригодятся не только в учебе, но и в реальной жизни. Рассуждая логически, ребенок может грамотно выразить свое мнение, подойти к решению той или иной задачи более осознанно, дать обоснование всевозможным явлениям, быстро сориентироваться в ситуации.
Поэтому решение логических задач должно быть неотъемлемой частью детского развития и образования. А для того, чтобы щелкать их как орешки, нужно понимать, какими приемами и методами пользоваться при решении.
Самое главное в решении логических задач
Почти у любой задачи есть несколько вариантов решения. Чтобы легко справляться даже с самыми непростыми заданиями, надо знать, какой способ будет наиболее подходящим в той или иной ситуации.
Понимание разных методов позволяет находить оптимальный вариант решения, что особенно важно в условиях ограниченного времени.
Все задачи на развитие логики можно разделить на группы:
- Математические ребусы;
- Задачи на истинность утверждений;
- Задачи на перемещение, взвешивание или переливание;
- Задачи, которые решаются с конца;
- Работа с множествами;
- Задачи на сопоставление «Кто есть кто?»
Выбор способа решения зависит от того, к какой группе относится задание.
Известные техники решения логических задач
- Табличный метод (таблицы соответствий, истинности, совмещенные, кубические):
таблицы создают наглядность, прозрачность рассуждений, помогают сделать верные выводы. - Применение законов из алгебры логики: вводятся обозначения для простых высказываний и преобразовываются в некую формулу.
- Метод рассуждений: подходит для решения простых задач с небольшим количеством объектов. Последовательное рассуждение над каждым условием задачи приводит к правильному выводу.
- Черчение блок-схем: способ, подходящий для решения задач на переливание, взвешивание. Рисуется схема, на которой отмечают последовательность действий и результат, полученный при их выполнении.
- Графический метод: подходит для решения задач на объединение или пересечение множеств. Самый популярный графический метод называется «Круги Эйлера». Нарисованная геометрическая схема наглядно показывает отношение между множествами.
- Метод «математический бильярд»: используется для решения задач на переливание жидкостей. Вычерчивается траектория движения бильярдного шара, который отталкивается от бортов стола в форме параллелограмма.
Рассмотрим подробно самые распространенные способы, которые могут использовать в решении логических задач ученики начальных классов:
Табличный метод
Условия задачи и результаты записываем в специальную таблицу. На пересечении строк и столбцов ставим «+», если утверждения не противоречат друг другу и «-», если они расходятся.
Задача:
У Сони, Маши, Антона, Кости и Юры есть домашние животные. У каждого из ребят живет или собака, или кошка, или попугай. Вот только девочки собак не держат, а у мальчиков нет попугаев. У Сони и Маши разные питомцы, а вот у Маши с Антоном – одинаковые. У Сони нет кошки. У Кости с Юрой живут одинаковые животные, а у Антона с Костей – разные. Какие животные живут у каждого?
Решение:
Чертим таблицу, где названия столбцов – имена ребят, а названия строк – животные. Ставим в каждой ячейке знаки «+» или «-», опираясь на условия задачи:
1. Девочки собак не держат (ставим «-» на пересечении этих ячеек).
2. У мальчиков нет попугаев (в этих ячейках тоже ставим «-»).
3. У Сони нет кошки (ставим «-»).
4. Значит, у Сони есть попугай (ставим «+»).
5. У Сони и Маши разные питомцы. Получается, у Маши нет попугая (ставим «-»), зато есть кошка (ставим «+»).
6. У Маши с Антоном одинаковые животные. Значит, у Антона тоже живет кошка (ставим «+») и нет собаки (ставим «-»).
7. У Антона с Костей разные питомцы, выходит, что у Кости нет кошки (ставим «-»), зато есть собака (ставим «+»).
8. У Кости с Юрой одинаковые животные, значит у Юры тоже собака (ставим «+»), а не кошка (ставим «-»).
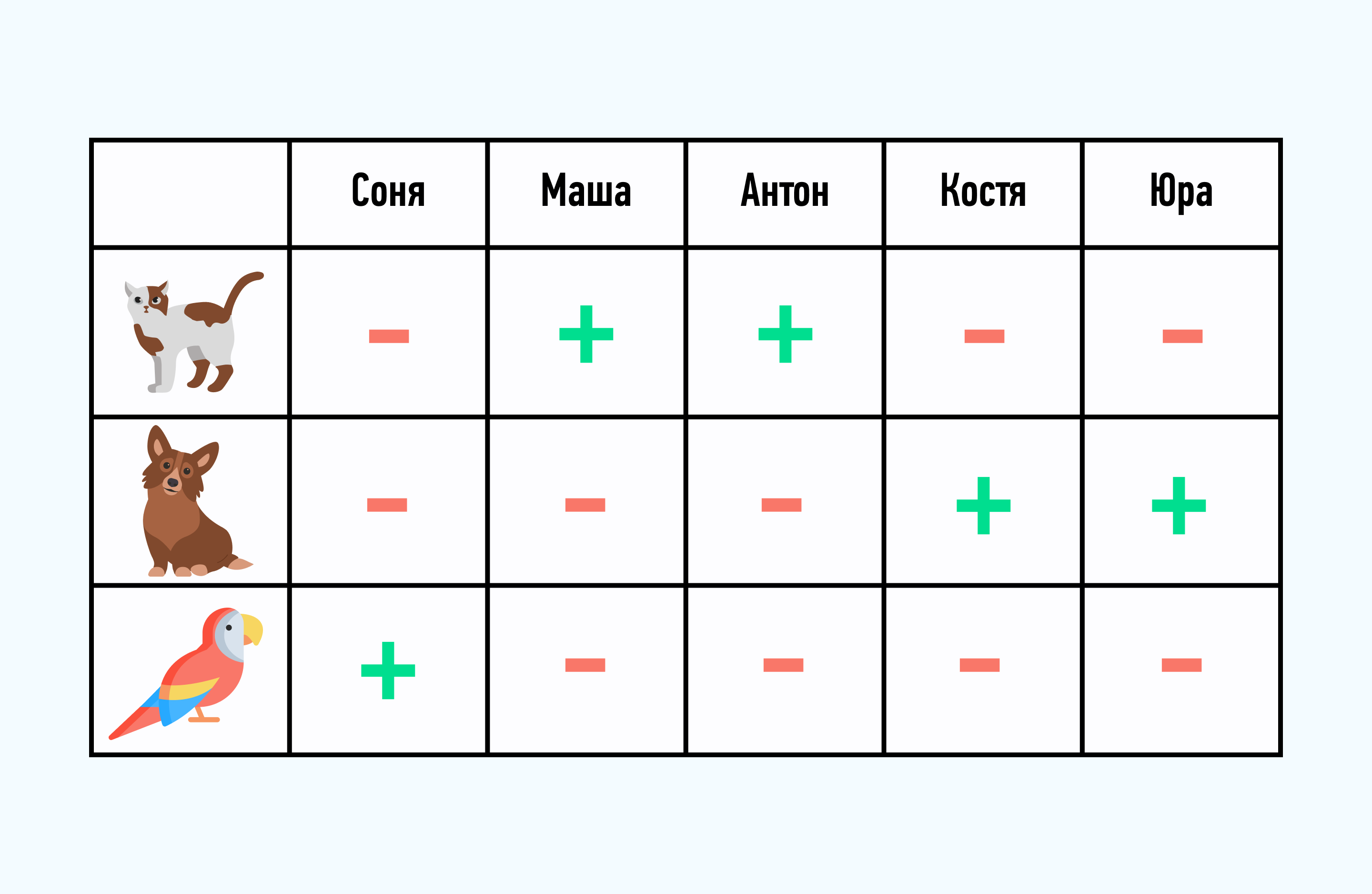
Так мы узнали, какие питомцы живут у каждого из ребят (ячейки со знаком «+»).
Ответ: У Сони попугай, у Маши и Антона кошки, у Кости и Юры собаки.
Круги Эйлера
Чтобы было легче разобраться в условиях задачи и найти решение, чертим круги, каждый из которых – отдельное множество.
Задача:
Всему классу задали на лето читать книжки. В списке литературы были такие произведения, как «Робинзон Крузо» Даниэля Дефо и «Белый клык» Джека Лондона. Известно, что 15 человек из класса прочитали «Робинзон Крузо», а остальные 11 – «Белый клык». Но среди них были 6 ребят, которые прочитали обе книги. Сколько человек прочитало только «Белый клык»?
Решение:
Чертим два круга, каждый из которых – множество детей, прочитавших определенную книгу, а пересечение кругов – дети, прочитавшие обе книги.
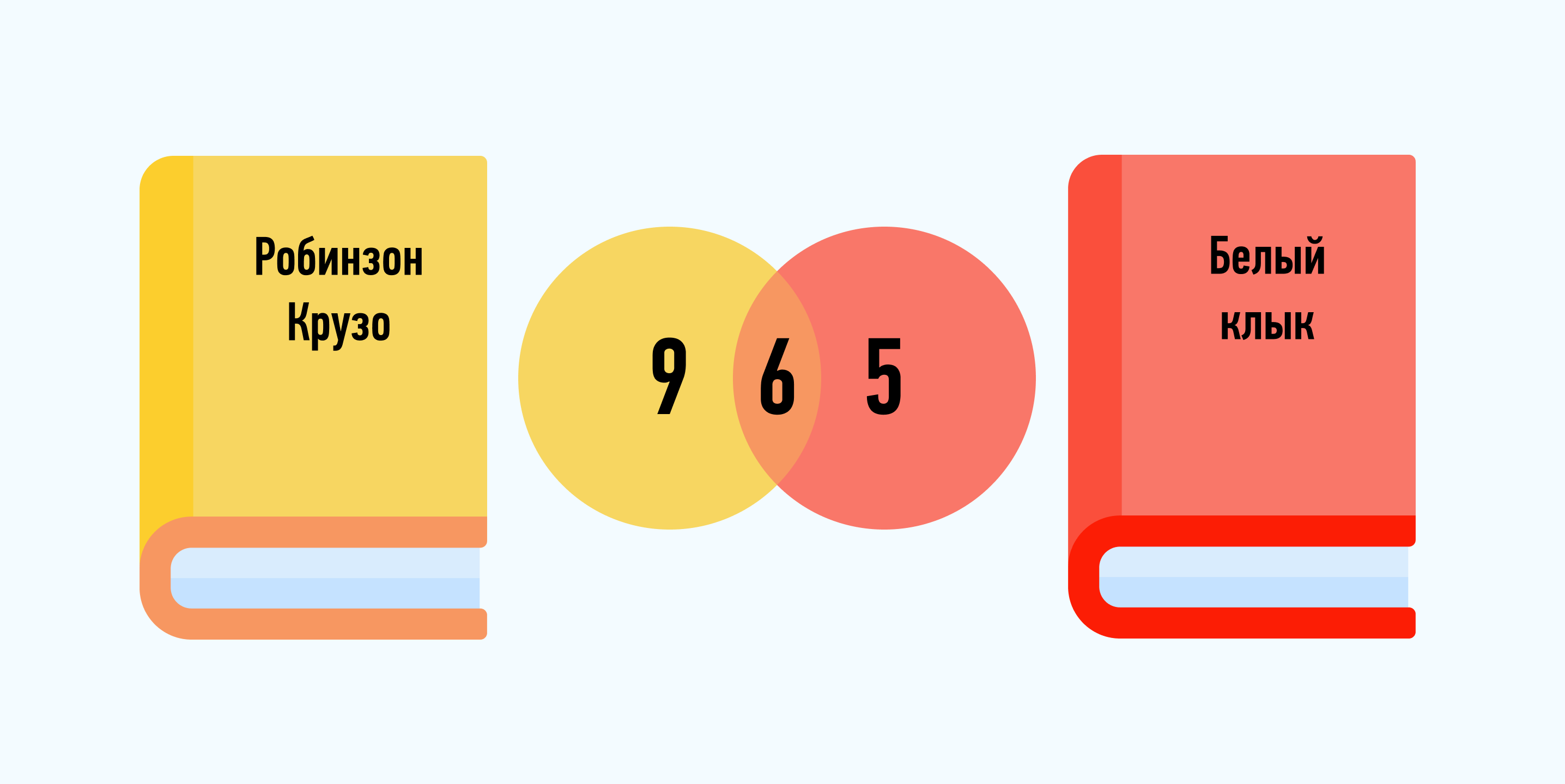
1. 15 – 6 = 9 – дети, которые прочитали только «Робинзон Крузо».
2. 11 – 6 = 5 – дети, которые читали лишь «Белый клык».
Ответ: 5 человек.
Метод рассуждений
Поочередно рассматриваем каждое из условий задачи и делаем логические выводы.
Задача:
На столе стоят вазы: голубая, зеленая, розовая и оранжевая. Третьей в ряду стоит та ваза, название цвета которой содержит больше всего букв. А зеленая стоит между оранжевой и розовой. Какая ваза стоит последней?
Решение:
1. Больше всего букв в слове «оранжевая», значит она третья по счету.
2. Если зеленая ваза стоит между оранжевой и розовой, значит, она будет второй в ряду, так как если ее поставить четвертой, то не останется места для розовой.
3. Соответственно, розовая будет стоять первой.
4. Остается голубая, она будет четвертой, то есть последней.

Ответ: голубая ваза.
Метод рассуждений «с конца»
Начинаем раскручивать клубок с конца, а затем сопоставляем результат с условиями задачи.
Задача:
Маме, папе и сыну вместе 125 лет. Когда родился сын, маме был 21 год. А папа старше мамы на 2 года. Сколько лет сейчас каждому из них?

Решение:
1. 21+2= 23 — было папе ( значит вместе родителям было 44 года)
2. (125 — 44) : 3 = 27 — возраст сына
3. 27 + 21 = 48 — возраст мамы
4. 48 + 2 = 50 — возраст папы
Ответ: 27, 48 и 50 лет.
Мы рассмотрели самые популярные и доступные методы, с помощью которых можно легко справиться с заданием. Главное – подобрать подходящий способ решения, который быстро приведет к правильному результату.
Для этого необходимо регулярно практиковаться и развивать свои способности. Отточить навыки решения подобных логических задач и многих других вы можете с помощью образовательной онлайн-платформы «Умназия».
Попробуйте решить вместе с ребенком задачу из раздела «логика» и переходите к регулярным занятиям на тренажере
Поробуйте решить задачу Умназии прямо сейчас!
Попробовать
Математика
Умназисты соревновались в поедании пирожков. Соревнование длилось ровно 45 минут. За это время все соревнующиеся в сумме съели 179 пирожков.
Посмотри на информацию о соревнующихся на рисунке. Можешь ли ты сказать, кто из умназистов занял почётное третье место?

Выбери ответ:
Третье место заняла Ума Коала.
Третье место занял Мышлен.
Третье место занял Грамотигр.
Третье место занял Ква-Квариус.
Третье место заняла Сообразебра.
ответить
Логика решения:
Мы знаем, что Мышлен ел по 1 пирожку в минуту, значит за 45 минут соревнования он съел 45 пирожков (1 х 45 = 45).
Если Мышлен съел на 10 пирожков больше, чем Сообразебра, то Сообразебра съела 35 пирожков (45 – 10 = 35).
Если Ума-Коала съела на 5 пирожков меньше, чем Сообразебра, то Ума-Коала съела 30 пирожков (35 – 5 = 30).
Чтобы выяснить, сколько съели Грамотигр и Ква-Квариус, сложим все пирожки, которые съели Мышлен, Ума-Коала и Сообразебра. Получается 45 + 35 + 30 = 110 пирожков.
От общего количества съеденных пирожков вычтем съеденное тремя умназистами: 179 – 110 = 69. Значит, Ква-Квариус и Грамотигр вместе съели 69 пирожков.
Из условия мы знаем, что Грамотигр съел пирожков в 2 раза больше, чем Ква-Квариус.
Допустим, Ква-Квариус съел 23 пирожка, тогда Грамотигр съел в два раза больше, то есть 23 х 2 = 46 пирожков.
Теперь снова сложим их пирожки, чтобы проверить себя: 23 + 46 = 69. Сходится.
Значит, Грамотигр (46 пирожков) занял первое место, Мышлен (45 пирожков) – второе, а Сообразебра (35 пирожков) – третье.
Если вам понравилось, было весело интересно и полезно, то ждем вас на нашей онлайн платформе!
Умназия сегодня — это:
1. Онлайн тренажер развития навыков мышления — логики, внимания, эрудиции.
2. Программа «Культурный код» по развитию кругозора. Для самых любознательных и тех, кого кажется уже ничем не удивить!
3. Курсы развития памяти. Хотите чтобы Ваш ребенок без труда учил стихи, запоминал иностранные слова и всегда помнил про день рождения бабушки? На курсах покажем и расскажем как же этого достичь.
4. Пять ступеней финансовой грамотности. Увлекательная история героя, которая полностью зависит от действий ребенка и не имеет определенного результата. Сможет ли он пройти все финансовые ловушки и освоить пятую ступень?
Ждем вас, будет весело и интересно!


Развитие логики у детей 7-10 лет
Развиваем критическое нестандартное мышление, учим работать с информацией и принимать верные решения
узнать подробнее
Читайте также:
- 15 сложных загадок на логику
- Загадки на логику с подвохом
- Логические загадки для детей
- Смешные логические загадки
- Загадки Эйнштейна на логику
Источник
