Развитие интеллекта у ребенка на уроке математики
Что такое интеллект? Приведем несколько определений
Интеллект — это ум, рассудок, разум, мыслительная способность человека.
Интеллект — это совокупность способностей, дающих возможность качественно выполнять умственную работу.
Интеллект — это обучаемость, то есть способность усваивать и самостоятельно добывать знания.
И, наконец, интеллект — это способность решать комплексные проблемы при изменяющихся обстоятельствах.
Условно можно вычленить следующие виды интеллекта:
- вычислительный;
- речевой;
- пространственный;
- практический;
- эмоциональный и социальный;
- а также музыкальный и творческий (прил. 1).
Несколько слов о каждом из этих видов и о том, насколько успешно они развиваются на уроках математики.
Вычислительный интеллект (или логико-математическая одаренность) это:
- это умение анализировать абстрактные задачи;
- это умение мыслить логически;
- это умение решать задачи в форме математических уравнений;
- это умение быстро находить числовые закономерности и применять их для решения задач.
Эти способности являются существенной предпосылкой для развития многих отраслей науки, так как математические основы лежат в фундаменте многих других наук. Действительно, если еще два столетия назад применение математики в физике было весьма относительно, в химии — в виде простейших уравнений первой степени, в биологии и вовсе равнялось нулю, то теперь же применение математики в этих науках неоспоримо значительно. Приложения математики широко распространяются также на область экономики и других специальных наук, начинают использоваться в языкознании и медицине. Этот вид интеллекта развивается на уроках математики абсолютно, более того, на каждом уроке необходимо пытаться воздействовать на развитие всех видов математических способностей, о которых речь пойдет немного позже.
Речевой интеллект
Этот вид интеллекта связан с целым спектром речевых явлений:
- словарным запасом;
- чувством языка;
- быстрым распознаванием и запоминанием слов и фраз;
- дифференцированным и точным выражением своих мыслей.
Чем выше речевой интеллект, тем легче у человека получается целенаправленное общение, тем легче человеку управлять своей жизнью, как профессиональной, так и личной. Наличие речевого интеллекта — непременное условие для педагогов, журналистов, и т.д. — для всех, кто ежедневно использует речь как орудие труда. И на развитие речевого интеллекта необходимо обращать особое внимание на уроках математики — здесь важно развивать культуру речи при доказательствах теорем, обосновании решений, применении математических понятий.
Пространственный интеллект
Способность восприятия оптических структур и двух- или трехмерных объектов. В чем он выражается? Это:
- умение выстраивать геометрическое тело или деталь по их схематическим изображениям;
- умение «видеть» двухмерные изображения в пространстве и сопоставлять в уме отдельные оптические структуры и построения;
- способность найти дорогу в незнакомом здании или городе по схемам и картам.
Развиваем ли мы на уроках пространственный интеллект? Безусловно! Стереометрия — потрясающий по своей мощи раздел математики, направленный стопроцентно на развитие пространственного интеллекта.
Практический интеллект
Этот вид интеллекта подразумевает способность координировать действия и умственную работу. Практический интеллект помогает контролировать тонкую моторику, которая требуется, например, при игре на скрипке, при вдевании нитки в иголку или при создании скульптуры. Развитие этого вида моторики особенно важно в первые 10 лет развития ребенка, когда глаза, руки и мозг работают в едином ритме. Связь тонкой моторики с общим развитием мозга очевидна. В математике задания, которые способствуют развитию практического интеллекта, — это различные задачи на прохождение лабиринтов, выбор кратчайшего пути, создание моделей многогранников и т.д.
Эмоциональный и социальный интеллект
Этот вид интеллекта очень много значит во всех областях жизни. В основном, это способность понять чувства других в общении. Более конкретно эмоциональный и социальный интеллект охватывает следующие основные способности:
в эмоциональной сфере:
- не позволять своим чувствам переливаться через край;
- сознательно влиять на свое поведение;
- пользоваться чувствами позитивно;
- действовать на основании этого.
в социальной сфере:
- умение общаться с другими людьми;
- находить общие точки соприкосновения;
- признавать чувства других людей;
- уметь представить себя на месте другого человека;
- способность осуществлять свои собственные желания, добиваться поставленной цели.
Таким образом, эмоциональный и социальный интеллект оказывает как в профессиональной, так и в личной жизни решающее влияние на качество жизни и способность преодолевать жизненные трудности. Кстати, научными изысканиями установлено, что успех человека в школе и на работе только на 20% связан с его IQ, определяемым тестами. В остальном — это его пригодность к социальным контактам, умение понимать чувства коллег и друзей. Можем ли мы развивать этот вид интеллекта на уроках? Конечно, не только можем, но и обязаны! Здесь уже на первый план выходит личность учителя, атмосфера, которую он создает на уроках, стиль его взаимоотношений с учениками, и недооценивать этот вид интеллекта нельзя.
Музыкальный и творческий интеллект
Под этим видом интеллекта подразумевается, прежде всего, способность развивать новые идеи, создавать новые проекты. Творческие способности имеют прямое отношение к изобретательности и душевной гибкости. Музыкальный интеллект тесно связан со слуховой памятью и различением высоты тона, с чувствами ритма и времени. Область применения творческих способностей ни в коей мере не ограничивается классическими видами творческой деятельности, такими, как труд художника или композитора, так как разрабатывать новые идеи выгодно в любой профессии.
Пожалуй, это единственный вид интеллекта, который мы на уроках развиваем менее всего. Однако если предложить учащимся создать какую-то трехмерную модель, удовлетворяющую начальным условиям (объем, площадь поверхности, форма или сочетание форм геометрических тел), или выполнить дизайнерское решение ландшафта при заданных параметрах площади или цветовой гаммы — вот тут и начнется полет фантазии и творчества!
(А еще можно заметить в скобках, что есть градация, и тоже весьма условная, на мужской и женский интеллект, интеллект «хитрого мужика» и рассеянного профессора, интеллект узкой профессиональной направленности и интеллект широкой эрудиции — видов и типов интеллекта великое множество, как и форм организации мыслительной деятельности человека).
Итак, если подытожить все вышесказанное, отвечая на вопрос «ЧТО?», вспоминается классическая фраза А.П. Чехова: «В человеке все должно быть прекрасно: и лицо, и одежда, и душа, и мысли». Воздействуя на различные виды интеллекта, и развивая их, учитель способствует развитию гармонично развитой личности, что и является основной задачей школы.
Как развивать интеллект учеников на уроках математики
А теперь поговорим о том, как развивать данные виды интеллекта на уроках. В принципе, интеллектуальный уровень развития личности определяется, прежде всего, двумя факторами: объемом приобретенной информации (это эрудиция) и способностью использовать эту информацию (это уже непосредственно интеллектуальное развитие личности).
Воздействуя на различные виды интеллекта, мы развиваем способности и мышление ученика. В свою очередь способности и мышление тоже имеют градации, — они указаны в приложении 1.
Остановимся подробнее на развитии математических способностей, которые разделяются на алгоритмические, геометрические и логические.
- Алгоритмические способности — это умение использовать, в первую очередь, определенные «шаблоны» для решения задач в конкретной ситуации, умение разбивать решение на элементарные составляющие, это способность применять аналитические методы, относящиеся к алгебре, математическому анализу, аналитической геометрии. Эти способности проявляются, например, при разложении многочленов на множители, построении графиков функций и их исследовании, решении уравнений, преобразовании выражений.
- Геометрические способности — это способность к пространственным представлениям и к введению геометрической наглядности при изучении математических проблем, это способность извлечь информацию из заданной конфигурации путем ее анализа и дополнения методом вспомогательных рисунков, дополнительных построений, мысленного анализа. Образно говоря, алгебра развивает навык, геометрия — воображение.
- Логические способности выражаются в вычленении из некоторого общего положения частных случаев и их исследовании, в создании экономной, непротиворечивой и оптимальной схемы решения задачи (и в выработке стратегии этого решения), в проведении доказательных рассуждений, с использованием приемов доказательства «от противного», продвижение при решении задач «от конца к началу», обращение к контрпримеру, и других.
Какие задачи развивают ту или иную способность? В приложении 2 представлены (конечно, весьма условно) различные типы задач, которые по-разному воздействуют на ум, рассудок и разум при различных типах мышления, которое тоже, в свою очередь, по форме и характеру решения задач может подразделяться на конкретное (предметное), абстрактное (образное) и интуитивное (вербально-логическое). Мышление развивается на протяжении всей жизни человека и по мере развития интеллекта претерпевает изменения: от конкретного, наглядно-действенного (достать игрушку, собрать пирамидку) к абстрактно-интуитивному (индуктивные и дедуктивные умозаключения, аналогии).
Сам предмет «математика» одним фактом своего изучения уже есть мощное средство для развития интеллекта, и, как следствие, — мышления и способностей ученика. А если еще разбавить «рутину» решаемых примеров и задач нестандартными упражнениями, уделив им пару минут урока — уровень воздействия станет в разы выше.
Например, для развития вычислительного интеллекта во время устных упражнений можно предлагать учащимся упражнения на нахождение недостающего элемента числовой цепочки (15, *, 17, 23, 19, 25 — очевидно, это число 21) или задачи на развитие логического мышления (У Смирновых в доме живут разные животные. Они могут быть кошками, собаками или хомяками. Известно, что:
- все животные, кроме двух — хомяки;
- все животные, кроме двух — кошки;
- все животные, кроме двух — собаки.
Какие животные, и в каком количестве проживают в доме Смирновых?
Ответ: трое животных — кошка, собака и хомяк.)
Развитие речевого интеллекта напрямую связано с развитием общей эрудиции, зрительной и слуховой памятью — тут уместны упражнения на воспроизведение конечного ряда слов или понятий за определенное время, нахождение словесной пары по ассоциациям (темный-светлый как широкий – ?), исключение лишнего из общего (палтус, сельдь, камбала, дельфин, акула — лишний дельфин, это млекопитающее), ну и упоминаемые уже доказательства теорем и обоснование решений.
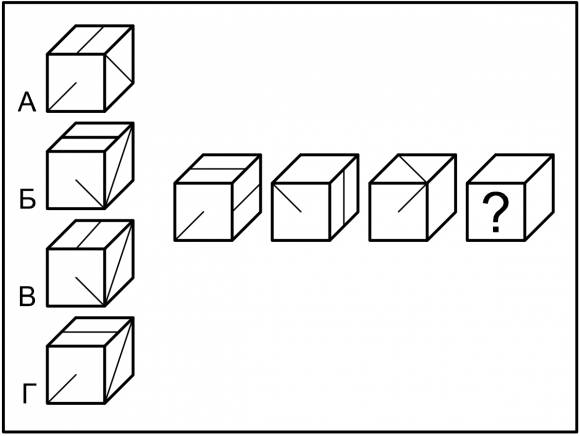
Развитию пространственного интеллекта способствуют упражнения на сочетание и перемещение фигур и геометрических тел, например, на нахождение положения кубика при определенных поворотах модели (на рисунке правильный ответ — В), на нахождение лишних фигур, распознавание оптических моделей.
Практический интеллект оперирует зрительными образами. Для его развития хороши упражнения на координацию моторики (игра Танграм), прохождение лабиринтов, нахождение оптимального пути из одного пункта в другой (теория графов).
В приложении 3 можно найти самые разнообразные упражнения на развитие применение различных типов мышления и интеллекта, а в целом — это просто разминка и толика удовольствия в этом увлекательнейшем деле — тренировке мозга.
Интеллектуальное развитие школьников на уроках математики напрямую зависит от личности учителя. Ученикам должно быть интересно на занятиях, будь то урок, факультатив или викторина, они должны почувствовать рост своих возможностей.
Приложения скачать >>>
Литература:
- Йорг Б.Тайлакер, Ульрих Визингер. Тренировка IQ. Ваш путь к успеху. Москва, АСТ Астрель, 2004.
- Кен Рассел, Филип Картер. IQ тесты. Москва, ЭКСМО, 2003.
- В. Коневская. От теории педагогики к практике развития творческих способностей учащихся. https://www.experts.in.ua/baza/analitic/index.php?ELEMENT_ID=33324
Об авторе: Лапицкая Татьяна Викторовна, учитель математики, Государственное учреждение образования “Средняя школа №16 г. Гродно”.
Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
Есть мнение? Оставьте свой комментарий:
Источник
Учитель высшей
квалификационной категории
Караваева Р.В.
г. Нижневартовск
«Развитие интеллектуальных способностей учащихся на уроках математики»
Интеллект – в широком смысле – совокупность всех познавательных функций индивида: от ощущения и восприятия до мышления и воображения; в более узком смысле – мышление.
Известна следующая история с графом Сергеем Юльевичем Витте. После окончания университета он не мог найти себе работы, соответствующей его квалификации, и пошёл работать начальником участка железной дороги. Во время прохождения царского поезда он посмел ослушаться распоряжения царя увеличить скорость поезда: знал, что это грозит крушением. А через месяц близ Харькова с царским поездом произошла катастрофа из-за бездумного рвения тамошних начальников. После этого Витте был назначен министром путей сообщения. Кто же такой был Витте? Оказывается, он закончил физико-математический факультет Одесского университета. Замечу, что в приведённом эпизоде ему ни в коем случае не нужно было его математическое образование. Просто он сумел принять самостоятельное решение в создавшейся ситуации. Вот это и есть математическое мышление . Именно это, а не знание логарифмов, тригонометрии и прочих – на первый взгляд скучных вещей- состоящих преимущественно из таблиц и формул. «Сила Витте заключалась вовсе не в применении математики, а в способе мышления, который заставляет человека с математическим образованием думать обо всех реалиях окружающего мира с помощью сознательного или бессознательного мягкого математического моделирования»-это мнение академика В.И.Арнольда.
Мышление является основной формой познания человеком действительности. Формирование интеллекта происходит в процессе целенаправленной деятельности; основа развития интеллекта – труд.
Общепризнано, что развитие интеллекта у школьников связано с формированием приёмов мышления, которые особенно ярко проявляются при обучении математике. Развитая психологами типология мышления выделяет такие виды как абстрактное и конкретное, речевое и эмоциональное, логическое , алгоритмическое. Широкое распространение получил термин «визуальное мышление», т.е. мышление, посредством зрительного восприятия. Каждый учитель использует на уроке наглядный материал – формулы и чертежи, плакаты и таблицы на стенах, модели и образцы в руках у учеников.
Вы написали на доске сложное алгебраическое выражение и предложили классу задание – упростить его. Ученики потянулись к
ручкам. Остановите их. Вспомните, что первым шагом в каждом этапе познания является «живое созерцание», добейтесь того, чтобы ученик внимательно рассмотрел предъявляемые ему зрительные образы. Для того, чтобы сделать «живое созерцание» действенным, ученик должен научиться анализу визуальной информации. Какие шаги сопровождают такой анализ? Прежде всего, должно произойти осознание общей структуры предложенного изображения (формулы, чертежа, графика, схемы и т.п.). При этом ученик мысленно пытается ответить на вопрос «на что?», т.е. на какое правило, на применение каких знаний нацелена поставленная задача. Вторая цель состоит в том, чтобы ученик увидел то, что заложено в данное задание.Далее происходит расчленение, зрительный анализ информации, узнавание отдельных фрагментов. Самым важным этапом визуального анализа является этап мысленного составления плана работы. Ученик должен определить порядок дальнейших действий, постараться в уме свернуть некоторые из хорошо знакомых ему операций, осуществить прогонку вариантов. Очень полезно обсуждать вслух, не производя вычислений, возможные варианты работы с прогнозированием того, что может получиться в
результате каждого из них.
Традиционно понимаемая учебная деятельность практически не в состоянии продвинуть нас в решении задачи формирования мышления. Математические знания учащихся слишком часто оказываются формальными и невостребованными, а у основной массы учащихся не формируется разумный подход к поиску решения незнакомых задач.
Каждому учителю необходимо активно изучать уже разработанные методики и рекомендации, направленные на развитие навыков в применении общих форм математической деятельности, таких, как:
* использование известных алгоритмов, формул;
* преобразование, интерпретация, кодирование;
* классификация и систематизация;
* правдоподобные рассуждения;
* выдвижение и проверка гипотез, доказательство и опровержение;
* разработка алгоритмов.
Рассмотрим несколько задач разного уровня сложности, решение которых способствует развитию у учащихся навыков в использовании некоторых из выделенных выше общих форм математической деятельности.
Использование известных алгоритмов, формул.
К сожалению, в преподавании математики доминирует формальный подход, связанный с отработкой конкретных методов решений. Но, если учащемуся предлагают упражнения только одного типа, выполнение каждого из которых сводится к одной и той же операции, если эту операцию не приходится выбирать среди сходных и условия, данные в упражнении, не являются для учащегося непривычными и он уверен в безошибочности своих действий, то учащийся перестаёт задумываться об их обоснованности. Подкреплю эти слова описанием следующей психолого-дидактической закономерности:
последовательность рассуждений А,В,С,…,К , повторяющаяся при решении однотипных задач, может свёртываться до ассоциации А,К. Однако, обратный процесс – развёртывание – происходит без потерь не у
всех учащихся. Этот эффект хорошо известен составителям вариантов ЕГЭ и вступительных экзаменов: какова бы ни была по сути проста задача, но если её решение предполагает использование двух различных ( хотя бы и известных алгоритмов ) или же если в нём должно содержаться некоторое исследование ( к примеру, по параметру), то массовые ошибки неизбежны. Более того, ошибки часто появляются и в том случае, если алгоритм используется в ситуации, в которой он неприменим.
Пример 1.
Решите систему
Решение этой задачи сводится к цепочке простых логических рассуждений и использованию стандартных формул. Однако, для получения правильного ответа, эти стандартные формулы следует правильно использовать. Не приводя ответ полностью, выпишу одну из четырёх серий решений:
(1)
К сожалению, слишком многие учащиеся бездумно отождествляют параметры и вместо серии (1) пишут, что
,
упуская тем самым, условно говоря, большую часть решений этой серии.
Пример2.
Некоторое число умножили на 3, а затем к полученному произведению прибавили 2. Верно ли, что полученное число больше исходного?
Ясно, что 3а + 2 > а только при а > -1, но какой процент восьмиклассников сразу даст верный ответ?
Несколько слов о такой форме математической деятельности, как кодирование, преобразование и интерпретация. Простейший пример – замена переменной, перевод задачи с одного математического языка на
другой. Кодирование или переформулирование способствует выявлению скрытых свойств объектов путём включения их в другую систему связей. Использование разнообразных формулировок задачи способствует её пониманию. Культура мышления предполагает развитое умение думать об одном и том же на разных языках. Важно научить школьников переформулировать задачи, переводить условия и результаты с одного языка на другой, т.е. кодировать информацию, т.е. интерпретировать
Самая первая кодировка, с которой знакомятся наши ученики в процессе обучения математике, – десятичная запись натуральных чисел.
Пример 3.
Докажите, что если от произвольного двузначного числа отнять двузначное число, записанное теми же цифрами в обратном порядке, то получится число, кратное девяти.
Если – исходное число. То = 10а +в, а число, записанное теми же цифрами в обратном порядке, равно =10в + а, поэтому их разность –= (10а + в ) – ( 10в + а ) = 9 ( а – в ) кратна девяти.
Пример 4.
Пусть Докажите, что
Данный интеграл можно вычислить явно:
После этого останется доказать, что ln2<. Тогда 2ln2+
Если калькулятор есть под рукой, то сразу получаем ln2
Но, если калькулятора нет, то надо ещё доказать, что
А это весьма проблемно, и требует дополнительных усилий.
Однако решение становится очевидным, если использовать геометрическую интерпретацию определённого интеграла как площади подграфика функции. Очевидно, что функция убывает на [1/2;1] и возрастает на [1;2], причём Поэтому подграфик функции f на отрезке [1/2;1] содержится в квадрате со стороной (см. рис. ), а потому его площадь действительно меньше, чем .
Это лишь несколько примеров задач, для решения которых требуется использовать различные типы интеллектуальной деятельности.
Всё содержание обучения, его направленность, все основные принципы обучения находят своё конкретное решение именно на уроке.
Главное условие развития учащихся – активная умственная деятельность,
в том числе и на уроке.
Как подвинуть учащихся к активной умственной деятельности на таком, казалось бы, скучном уроке, как уроке-лекции? Ребят можно заинтересовать, если показать ограниченность их знаний в тех аспектах, в которых они уверены; убедить их в расширении возможностей выполнять какие-либо трудные действия, рассказать интересные исторические сведения, показать применение материала лекции в тех или иных специальностях; высказать какое-либо нестандартное обещание; организовать деятельность учащихся таким образом, чтобы ребята самостоятельно «открыли» самую важную теорему предстоящей лекции; включить учащихся в диспут и т.п. Основная часть лекции сопровождается вопросами классу : «А как вы думаете? Предложите свои варианты. Приведите опровергающие примеры. Попробуйте доказать самостоятельно». Такие вопросы стимулируют учащихся к активной работе на лекции, помогают им не «выключаться» из процесса познания.
Очень важно создать такую атмосферу на уроке, когда ученики на боятся «ляпнуть глупость», задать любой вопрос или ,наоборот, дать ответ не во время. Способность задавать вопросы является верным признаком активной мыслительной деятельности.
Один из путей обеспечения образовательных результатов – совершенствование урока. А один из путей совершенствования урока – рациональное сочетание коллективной и дифференцированной работы.
Я стараюсь построить урок так, чтобы ученикам слабым уделить достаточно внимания, чтобы у них не появилось ощущение неполноценности из-за кажущейся непосильности задачи, а ученики творческого уровня при этом не потеряли бы интерес к учению.
Больше других от наших недоработок страдают наиболее способные учащиеся, те, кто в младших классах учился легко и радостно, у которых ,по словам Песталоции, «ум хочет мыслить», к 7 классу склонны потерять интерес к учёбе, если их познавательная деятельность оказывается недостаточно нагруженной, ибо усвоить стереотипы они могут без затруднений, а глубинные пласты мышления при этом бездействуют. И, если мы с вами не заботимся об их развитии, не поставляем им достаточную пищу для ума, то они не смогут состояться как творческие личности. Это быстрые, не терпящие «дрессировки» (натаскивания), отказывающиеся выполнять вычисления и тренинговые задания ребята. Для них необходима специальная работа ( и на уроке, и вне урока ) по развитию мыслительных способностей, настойчивости, самостоятельности и ответственности, их необходимо включать в творческую деятельность, предлагать задачи, направленные на формирование гибкости ума, учить их преодолению стереотипов мышления, методам обобщения, навыкам профессиональной работы с текстами.
Работа будет эффективной, если в систему работы класса будет включено проведение, как минимум один раз в месяц тренингов с последующим качественным анализом работ. Анализ работ не должен сводиться только к выставлению баллов и показу правильного решения – он должен включать разбор всех возможных способов решений задачи и сравнение этих способов с учётом их эффективности, эстетики и временных затрат. Особенно необходимо продумывать те варианты решений, которые не были реализованы школьниками и рассказать им об упущенных возможностях. Даже в достаточно продвинутых в математическом плане классах не следует упускать возможности анализа подобных задач.
Анализ содержания заданий ЕГЭ показывает, что появляются задачи, требующие специальной подготовки для их решения, а значит хорошо
развитого мышления, интуиции. При подготовке к ЕГЭ я обязательно учу ребят тому, как можно многие из заданий решить нетрадиционным
способом, сэкономив при этом время. Немаловажно, что успешное выполнение заданий первой части окрыляет учащегося, задаёт тон всей последующей работе, помогает успокоиться преодолеть экзаменационное напряжение.
Конечно, полные решения должны отрабатываться, но и другие варианты решений также неплохо знать и использовать для самоконтроля. Естественно, что задания с выбором ответа следует использовать постоянно. Но в контрольных работах необходимо предлагать задания, в которых учащиеся приводили полные решения, тем самым постепенно готовясь к выполнению заданий второй и третьей частей ЕГЭ.
Каждому учителю понятны объективные трудности, возникающие у учеников при переходе от теории к практике, т.е. при решении задач. В литературе рассматриваются различные подходы к обучению решению задач. Один из них построен на ключевых задачах. Эти задачи – своеобразные опоры для решения других. В том числе и нестандартных математических задач. Так как ключевые задачи предполагается использовать при работе со всеми учащимися, то в их число входят задачи, для решения которых известен алгоритм решения. Следовательно, вы вправе возразить: обучение алгоритмам слабо развивает мышление учеников. Но это не так.
Во-первых, общие методы должны опираться на алгоритмы решения типовых задач (без этого они не работают).
Во-вторых, перед школой стоит задача формирования алгоритмической культуры школьников.
В-третьих, разработка алгоритмов решения ключевых задач является творческой деятельностью, а значит, безусловно, способствует, а не тормозит развитию школьников. Наконец, нельзя забывать, что для успешного решения нестандартных математических задач важное значение имеет личный опыт учащихся, приобретённый ими в процессе обучения, а использование этого опыта особенно эффективно осуществляется путём узнавания в новых задачах последовательности ключевых задач. А эта деятельность не сводится к алгоритмической и безусловно свидетельствует о развитии мышления школьников.
Способности развиваются тем успешнее, чем чаще в своей деятельности человек добивается до потолка своих возможностей и постепенно поднимает этот «потолок» всё выше и выше.
Особое значение для развития детей имеют интеллектуальные игры. Опыт показывает, что игра, проведённая в дидактических целях, приносит не только хорошие результаты, но и много положительных
эмоций. Интеллектуальная игра – эффективная форма проведения
уроков математики, поскольку наиболее прочны те знания., которые приобретались с заинтересованностью. Любое интеллектуальное задание несёт в себе определённую умственную нагрузку, которая чаще всего замаскирована занимательным сюжетом, внешними данными, интересным условием.
Методику проведения интеллектуальных игр на уроках и во вне
урочное время предлагают на страницах журнала «Математика в школе», а также в различных, имеющихся в продаже книжных новинках.
Следует подчеркнуть важность составления различных интеллектуальных заданий самими учащимися ( придумать анаграммы, составить цепочку по заданному условию, построить числовой ряд, используя определённую закономерность возникновения последующих чисел, составить графический диктант и т.п.) Эта работа формирует определённые мыслительные операции: анализ-синтез, обобщение, абстрагирование, конкретизация, сравнение и т.п., что, несомненно, приносит успех в освоении учебного предмета.
Систематическое решение различных интеллектуальных задач формирует уверенность, вызывает желание участвовать в различных интеллектуальных играх и конкурсах. Опыт показывает, что участие в такого рода деятельности оказывается, в основном, победоносным. Уважаемые коллеги! Проявляйте инициативу в творчестве, в реализации поставленных задач. Отдавайте детям все свои знания, опыт, горячее сердце и тепло души. И результат не заставит себя ждать. А вот когда результат получен и ученик может гордиться своими достижениями, тогда мы с вами можем считать свою работу выполненной. Главное – добиться того, чтобы наши ученики думали, делали выводы, спорили, сомневались, работали.
Используемая литература:
Н.И. Зильберберг, «Урок математики: подготовка и проведение», М, «Просвещение»,АО «Учебная литература», 1996г.
И.С. Якиманская, «Развивающее обучение», М, «Педагогика», 1979г.
Р.Г. Хазанкин и др. «Математическая подготовка и развитие школьников в условиях ЕГЭ», Уфа, 2004г.
О.Б.Епишева, «Технология обучения математике на основе деятельного подхода»,М, «Просвещение»,2003г.
«Математика в школе», №3, 2015г.
Источник
